KIRCHHOFF’S LAW video
KIRCHHOFF’S VOLTAGE LAW
*For any closed path in a network, Kirchhoff’s voltage law (KVL) states that the algebraic sum of the voltages is zero
*Some of the voltages will be sosurces, while others will result from current in passive elements creating avoltage
* sum of voltage sources =sum of drop voltage
* sum of voltage sources -sum of drop voltage =0
for from the current direction as shown, we have
Va –Vb-V1-V2-V3 =0
Va-Vb= I(R1+R2+R3) =0
KIRCHHOFF’S CURRENT LAW
*The connection of two or more circuit elements creates a junction called a node
* The junction between two elements is called a simple node and no division of current results
* The junction of three ormore elements is called aprincipal node and here current division does take place Kirchhoff’s current law (KCL) states that the algrebraic sum of the currents at a node is zero
* It may be stated alternatively that the sum of the currents enteringa node is equal to the sum of the currents leaving that node
sum of current enter the node =sum of current out
∑ Ienter = ∑ Iout
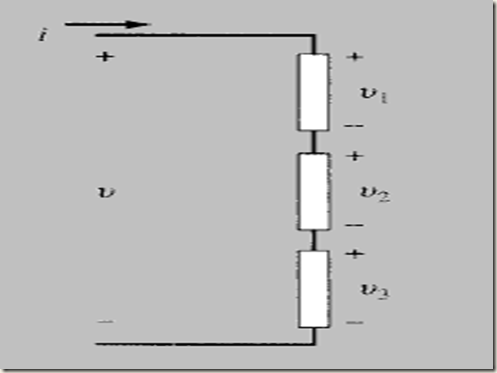
* CIRCUIT ELEMENTS IN SERIES
Three passive circuit elements in series connection as shown in Fig we have the same current i. The voltages across the elements are v1, v2, and v3The total voltage v is the sum of the individual voltages
v = v1 + v2 + v3
*CIRCUIT ELEMENTS IN PARALLEL
For three circuit elements connected in parallel as shown in Fig KCL states that the current i entering the principal node is the sum of the three currents leaving the node through the branches
VOLTAGE DIVISION*
set of series-connected resistors as shown in Fig is referred to as a voltage divider Theconcept extends beyond the set of resistors illustrated here and applies equally to impedances in series
CURRENT DIVISION
A parallel arrangement of resistors as shown in Fig results in a current dividerThe ratio of thebranch current i1 to the total current i illustrates the operation of the divider





No comments:
Post a Comment