Analysis Methods

THE MESH CURRENT METHOD

In the mesh current method a current is assigned to each window of the network such that thecurrents complete a closed loop. They are sometimes referred to as loop currents. Each element andbranch therefore will have an independent current. When a branch has two of the mesh currents, theactual current is given by their algebraic sum. The assigned mesh currents may have either clockwise or counterclockwise directions, although at the outset it is wise to assign to all of the mesh currents aclockwise direction. Once the currents are assigned, Kirchhoff’s voltage law is written for each loop toobtain the necessary simultaneous equations

EXAMPLE

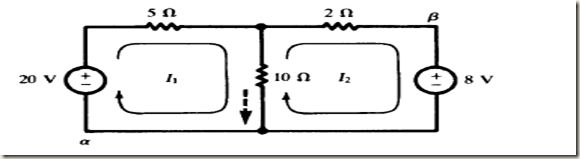
Obtain the current in each branch of the network shown in Fig.  using the mesh current method

                                                                        

 

The currents I1 and I2 are chosen as shown on the circuit diagramApplying KVL around the left loopstarting at point

 

-20 + 5I 1+10( I1-I2 ) = 0

8+10( I2 –I1 ) + 2I2         = 0

15I1 -10I2  = 20

-10I1 +12I2 = –8

 

I1 = 2A and I2 = 1 A. The current in the center branch, shown dotted is I1 - I2 = 1 A

 

KIRCHHOFF’S LAW videos

                                                                                                                        

 

 

KIRCHHOFF’S LAW

KIRCHHOFF’S  LAW video

  KIRCHHOFF’S VOLTAGE LAW  

*For any closed path in a network, Kirchhoff’s voltage law (KVL) states that the algebraic sum of the voltages is zero

 

*Some of the voltages will be sosurces, while others will result from current in passive elements creating  avoltage

* sum of voltage sources =sum of drop voltage

*  sum of voltage sources -sum of drop voltage =0

                            

                                                                                                                       for  from the current direction as shown, we have

Va –Vb-V1-V2-V3 =0

Va-Vb= I(R1+R2+R3) =0

 

KIRCHHOFF’S CURRENT LAW

*The connection of two or more circuit elements creates a junction called a node

* The junction between two elements is called a simple node and no division of current results

* The junction of three ormore elements is called   aprincipal node and here current division does take place Kirchhoff’s current law (KCL) states that the algrebraic sum of the currents at a node is zero

* It may be stated alternatively that the sum of the currents enteringa node is equal to the sum of the currents leaving that node

 

sum of current enter the node =sum of current out

                                           

                                                           

    

∑ Ienter = ∑ Iout

 

* CIRCUIT ELEMENTS IN SERIES

Three passive circuit elements in series connection as shown in Fig we have the same current i. The voltages across the elements are v1, v2, and v3The total voltage v is the sum of the individual voltages

 

v = v1 + v2 + v3

 

 

 *CIRCUIT ELEMENTS IN PARALLEL

For three circuit elements connected in parallel as shown in Fig KCL states that the current i entering the principal node is the sum of the three currents leaving the node through the branches 

  

 

                                                                                                     
                                                                                                                                                         VOLTAGE DIVISION*

                                       

                                                                                                                        set of series-connected resistors as shown in Fig is referred to as a voltage divider Theconcept extends beyond the set of resistors illustrated here and applies equally to impedances in series

                                       

                                                                                                                        CURRENT DIVISION

 

  A parallel arrangement of resistors as shown in Fig results in a current dividerThe ratio of thebranch current i1 to the total current i illustrates the operation of the divider